En Sergi em concedeix l'honor de publicar la resposta, si més no la resposta que jo proposo i a la qual vosaltres podeu fer tota mena de correccions i comentaris. M'estreno d'aquesta manera en l'exercici de colaborar amb aquest blog tan interessant i al qual tinc la il·lusió de plantejar preguntes en un futur proper; preguntes que de vegades no em deixen dormir, perquè sóc curiós de mena.
Pel que fa a la pregunta que ens porta avui fins aquí, haig de dir que representa un problema molt agradable que se'm va acudir a mi quan impartia física i ampliació de matemàtiques en una escola concertada a l'any 1998. L'enunciat feia així:
"Un noi camina per la sorra de la platja, clava els ulls a l'horitzó i observa la ratlla nítida que separa cel i Terra. A quina distància es troba aquesta ratlla?"
Les reaccions de l'alumnat no es varen fer esperar: incomprensió, sorpresa, intriga, escepticisme... Tot es va solucionar quan els vaig dir que la resolució del problema era de caràcter "voluntari", que no passava res si no el solucionaven, i que, en tot cas, si arribaven a descobrir la resposta, això voldria dir que tenien una gran capacitat analítica: que sabien concretar què se'ls demanava, que eren capaços d'establir quins valors s'havia de suposar que coneixien d'entrada, que fins i tot podien resoldre el problema amb uns valors d'entrada que no fossin xifres sinó lletres o conceptes, que podien convertir en equació tot allò que sabien referent a la geometria o a la geografia, i que sabien manipular de manera eficient les equacions i la seva mecànica. Un cop rebaixada la tensió i proposat l'enigma com un repte a les seves capacitats i no pas com una condició per aprovar, la incomprensió es va transmutar en esperança, la sorpresa en il·lusió, la intriga en curiositat i l'escepticisme en determinació.
Anem per feina.
Al principi sempre és convenient començar amb un dibuix:
Al principi sempre és convenient començar amb un dibuix:
He dibuixat un noi molt gran en comparació amb el planeta Terra, perquè d'aquesta manera resulta molt més fàcil percebre la idea que vull transmetre. Els raonaments seran igual de vàlids si el noi fa 1,8 metres d'alçada.
Al principi és important comprendre què volem dir quan parlem de la ratlla de l'horitzó. La ratlla de l'horitzó, tal com veieu en el dibuix, és el punt més llunyà de la superfície de la mar que el noi pot veure. Més enllà, no hi pot veure res, perquè la corba de la Terra li amaga el que hi ha al darrere. Més a prop, hi veu els punts de mar que estan entre la ratlla de l'horitzó i ell. Al dibuix superior, la ratlla de l'horitzó es veu com un punt vermell i no com una línia perquè en realitat l'estem mirant de perfil, i una línia vista per la punta es veu com un punt. Aquest punt es troba al punt de tangència amb la Terra de la recta que surt dels ulls del noi i que és tangent a la Terra. Si el noi fos més alt, o si es mira l'horitzó des d'una muntanya, el punt de tangència estaria més lluny. Si el noi s'ajeu a Terra, el punt de tangència està més a prop. Podeu fer diferents dibuixos per a comprovar-ho. Heus aquí doncs la primera metàfora que després si convé podríem analitzar. L'horitzó serà més proper (les nostres ambicions, anhels o desigs, seran més propers, més fàcils) com més ens arrosseguem per terra. L'horitzó serà més llunyà (els nostres anhels seran més costosos, més meritoris, més elevats, més a llarg plaç) com més ens aixequem sobre nosaltres mateixos i sobre la nostra pròpia alçada. I per últim, els nostres horitzons estaran allà a on s'ajuntin el cel i la Terra, a on el més espiritual coincideixi amb el més terrenal. Però bé, deixem les metàfores i tornem a la ciència.
Un cop veiem clar que la distància que volem calcular és la que uneix els ulls del noi amb el punt de tangència de la recta tangent a la Terra que surt dels seus ulls, observarem el següent dibuix per a disposar-nos a esbrinar pistes que ens condueixin a les equacions "salvadores":
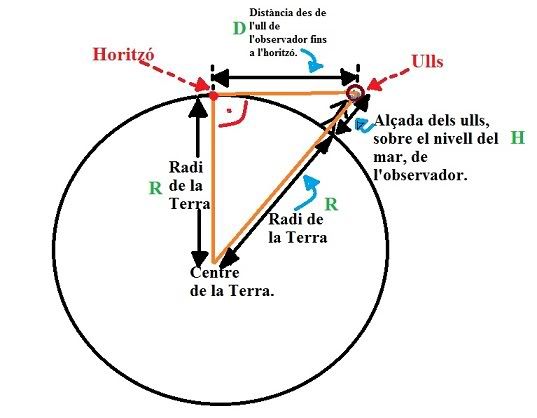

Sabem que la recta tangent a una circunferència és perpendicular al radi de la circumferència en el punt de tangència. És per això que, a l'horitzó, la recta D és perpendicular al radi R de la Terra. La recta D és la distància entre els ulls del noi i l'horitzó. Mirant el dibuix comprovem que es forma un triangle rectangle (el de color taronja) que té per catets D i R, i que té com a hipotenusa una recta que té per longitud la suma de R més l'alçada h dels ulls del noi sobre el nivell del mar.
Una possible relació entre aquestes tres distàncies ens la dona el teorema de Pitàgores que diu que la suma dels quadrats dels catets és igual al quadrat de la hipotenusa:
Com que el que volem trobar és D, l'aïllem i trobem que l'expressió que ens la proporciona és:
Suposem que l'alçada dels ulls sobre el nivell del mar, si el noi s'està mullant els peus amb les onades que van i vénen, sigui de 1,7 metres. El radi mitjà de la Terra és de 6371 quilòmetres. Si substituïm correctament aquests valors tenim que D val aproximadament 4654 metres, és a dir, l'horitzó, quan estem arran d'aigua, està a uns quatre quilòmetres i mig.
Us poso a continuació la distància a la qual es troba l'horitzó des de diversos punts emblemàtics; recordeu que com més alts estem, més lluny tenim l'horitzó. En alguns casos podem veure allò que està més enllà de l'horitzó, això passa quan l'objecte (muntanya, veler...) és prou alt com per treure la punta superior per damunt de l'horitzó, és a dir per damunt del punt de tangència de la recta que surt dels nostres ulls i que és tangen a la Terra. Si la visió fos nítida, això serviria per demostrar que la Terra està corbada. Si des del Tibidabo veiéssim només la punta superior del Puig Major de Mallorca, i ens restés oculta la part inferior, voldria dir que la part inferior ens queda amagada per la corba de la Terra.
Us poso a continuació la distància a la qual es troba l'horitzó des de diversos punts emblemàtics; recordeu que com més alts estem, més lluny tenim l'horitzó. En alguns casos podem veure allò que està més enllà de l'horitzó, això passa quan l'objecte (muntanya, veler...) és prou alt com per treure la punta superior per damunt de l'horitzó, és a dir per damunt del punt de tangència de la recta que surt dels nostres ulls i que és tangen a la Terra. Si la visió fos nítida, això serviria per demostrar que la Terra està corbada. Si des del Tibidabo veiéssim només la punta superior del Puig Major de Mallorca, i ens restés oculta la part inferior, voldria dir que la part inferior ens queda amagada per la corba de la Terra.
Els següents personatges o punts tenen l'horitzó als quilòmetres de distància descrits a continuació:
Noi a nivell del mar.......................................4,65
El vigilant de la platja assegut a la trona...... 7,98
El pis superior de la Torre Mapfre.................44,29
El Castell de Montjuich..................................46,9
El Tibidabo....................................................80,77
La Mola (Sant Llorenç del Munt)...................118,6
Puig Major (Mallorca)...................................135,7
El Canigó........................................................188,36
El Teide (Tenerife)..........................................217,7
Des d'un avió (a 11000 metres)......................374,54
Des del capdamunt de l'atmosfera.................619



Fantàstica resposta. Trobo que les anècdotes personals on parles dels teus alumnes enriqueixen molt l'explicació.
ResponEliminaAfegeixo un càlcul que he fet ara amb la fórmula:
Mont Olimp (Mart): 386,83 km.
Afegeixo al que has dit sobre els objectes més enllà de l'horitzó, que podríem calcular les distàncies de dues muntanyes a l'horitzó. Si la suma d'aquestes distàncies fos superior a la distància que separa les muntanyes, es podrien veure entre si. Negligint els efectes atmosfèrics, és clar.
Així podríem solucionar d'una vegada per sempre els mites aquells dels més vells del poble que sempre et diuen "en els dies clars, des d'aquest cim es veu Mallorca".
Gràcies per participar en aquest bloc, Jeremias. Esperem que tornis amb preguntes interessants ben aviat.